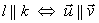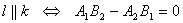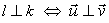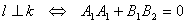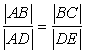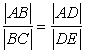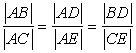| Kula |
|
||
|
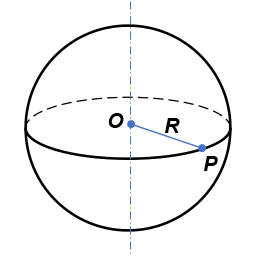
● Kula o środku O i promieniu R nazywamy zbiór wszystkich punktów przestrzeni, których odległość od punktu O jest niewiększa od R. ● Kula jest bryłą obrotową powstałą przez obrót półkola dookoła prostej, w której zawarta jest średnica tego półkola. |
|||
| Sfera | |||
|
● Sferą o środku O i promieniu R nazywamy zbiór wszystkich punktów przestrzeni, których odległość od punktu O jest równa R. ● Sfera jest bryłą obrotową powstałą przez obrót półokręgu dookoła prostej, w której zawarta jest średnica tego półokręgu. |
|||
| Wzory | |||
|
● Wzór na pole powierzchni kuli: P = 4π·R 2 |
● Wzór na objętość kuli:
|
||
| Koło |
|
|
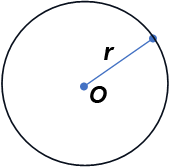
● Kołem o środku O i promieniu r nazywamy zbiór punktów płaszczyzny, których odległości od punktu O są mniejsze lub równe r. P - pole koła o promieniu r P = π·r 2 |
|
| Okrąg | |
|
● Okręgiem o środku O i promieniu r nazywamy zbiór punktów płaszczyzny, których odległości od punktu O są równe r. l - długość - obwód okręgu o promieniu r l = 2π·r |
|
| Długość łuku okręgu | |
|
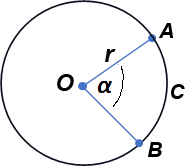
● Łukiem okręgu nazywamy każdą z dwóch części okręgu, na jaką dzielą okrąg dwa różne punkty tego okręgu. ł - długość łuku ACB ł = | ACB |
|
|
| Równania dwóch prostych l i k na płaszczyźnie | ||
|
l : A1 x + B1 y + C1 = 0 gdy: k : A2 x + B2 y + C2 = 0 i |
|
l : y = a1 x + b1
k : y = a2 x + b2
|
| Warunek równoległości prostych ( l || k ) | ||
|
|
a1 = a2 | |
| Warunek prostopadłości prostych ( l ⊥ k ) | ||
|
|
a1 · a2 = −1 | |
| Kąt φ między prostymi l i k | ||
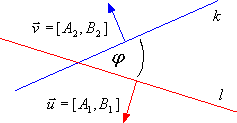 |
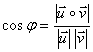 |
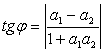 |
| Współrzędne punktu | ||
| punkty oznaczamy : A, B, C ... , A = ( xA ,yA ) - punkt A o współrzędnych xA , yA. | ||
| Na osi: | Na płaszczyźnie: | W przestrzeni: |
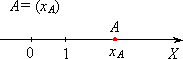 |
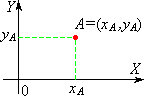 |
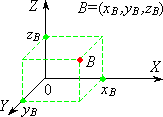 |
| Odległość między dwoma punktami | ||
| ● Odległość między dwoma punktami A i B oznaczamy symbolem |AB| | ||
| ● Dla dowolnych punktów A, B, C : | |
| |AB| ∈ R+ ∪ {0} | |AB| = |BA| |
| |AB| = 0 ⇔ gdy A = B | |AB| ≤ |AC| + |CB| ( nierówność trójkąta ) |
| ● Punkt C leży między punktami A i B , gdy |AB| = |AC| + |CB| | |||
| ● Trzy punkty A, B, C są współliniowe - to znaczy leżą na jednej prostej - jeśli spełniony jest jeden z trzech warunków: | |||
| lub |AB| = |AC| + |CB| |
lub |BC| = |BA| + |AC| |
||
| Odległość punktów w układzie współrzędnych | |||
| Na płaszczyźnie: | W przestrzeni: | ||
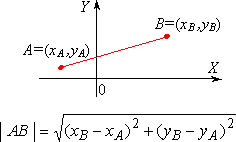 |
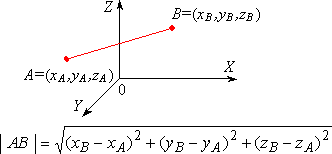 |
||
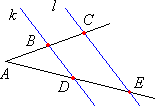
| Twierdzenie Talesa | ||
|
● Jeżeli ramiona kąta przetniemy dwoma prostymi równoległymi, to długości odcinków wyznaczonych przez te proste na jednym ramieniu kąta są proporcjonalne do długości odpowiednich odcinków wyznaczonych przez te proste na drugim ramieniu kąta. |
||
|
|
● ● |
● |
|
● Twierdzenie odwrotne do twierdzenia Talesa: |
||