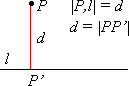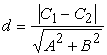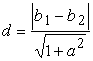| Odległość punktu od prostej | |
|
● Odległość d punktu P od prostej l jest równa odległości tego punktu od jego rzutu prostokątnego P' na prostą l. |
|
| Odległość punktu od prostej w układzie współrzędnych na płaszczyźnie | |
|
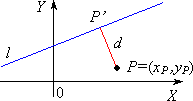
równanie prostej l : Ax + By + C = 0 gdzie A 2 + B 2 > 0 Jeżeli | P,l | = | PP' | = d , to
|
|
| Definicja odcinka | |
|
● Odcinkiem AB nazywamy figurę utworzoną z punktów A i B, zwanych jego końcami, oraz wszystkich punktów leżących między nimi na prostej wyznaczonej przez te punkty ( lub: odcinek to część prostej ograniczona dwoma punktami, razem z tymi punktami ). ● Jeżeli A = B to odcinek AB nazywamy odcinkiem zerowym. |
|
| Osie symetrii odcinka na płaszczyźnie | |
|
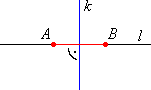
● Na płaszczyźnie odcinek niezerowy AB ma dwie osie symetrii: prostą w której się zawiera i prostą zwaną symetralną. ( na rysunku osie symetrii odcinka AB to proste l i k ) |
|
| Osie symetrii odcinka w przestrzeni | |
|
● W przestrzeni odcinek ma nieskończenie wiele osi symetrii. |
|
| Symetralna odcinka | |
|
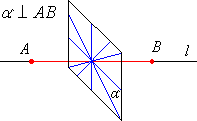
● Symetralną niezerowego odcinka AB nazywamy prostą prostopadłą do tego odcinka i przechodzącą przez jego środek. ● Symetralna odcinka jest tą osią symetrii odcinka, w której nie jest on zawarty. ● Symetralna odcinka niezerowego jest zbiorem wszystkich punktów płaszczyzny, których odległości od końców tego odcinka są równe. |
|
| Figura płaska |
|
● Każdy zbiór punktów płaszczyzny nazywamy figurą. ● Figura płaska jest ograniczona, gdy istnieje koło, w którym ta figura się zawiera. ● Figura płaska jest nieograniczona, gdy nie jest zawarta w żadnym kole. |
| Figura przestrzenna |
|
● Każdy zbiór punktów przestrzeni nazywamy figurą przestrzenną. ● Figura przestrzenna jest ograniczona, gdy istnieje kula, w której ta figura się zawiera. ● Figura przestrzenna jest nieograniczona, gdy nie jest zawarta w żadnej kuli. |
| Figura wypukła |
|
● Figurę nazywamy wypukłą jeżeli każdy odcinek, którego końce należą do figury zawiera się w tej figurze. |
| Figury przystające |
|
● Figury f1 i f2 nazywamy figurami przystającymi ( f1 ≡ f2 ), gdy istnieje izometria przekształcająca figurę f1 |
| Figury podobne |
|
● Figury f1 i f2 nazywamy figurami podobnymi ( f1 ~ f2 ), gdy istnieje podobieństwo przekształcające figurę f1 |
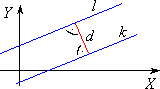
| Odległość prostych równoległych w układzie współrzędnych | |
|
d = | l, k | - odległość prostych równoległych l i k Jeżeli l : Ax + By + C1 = 0 i k : Ax + By + C2 = 0 , to:
Jeżeli l : y = ax + b1 i k : y = ax + b2 , to
|
|