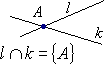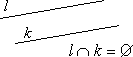| Proste przecinające się | |
|
● Prostymi przecinającymi się nazywamy proste, które mają dokładnie jeden punkt wspólny. |
|
| Proste równoległe | |
|
● Prostymi równoległymi nazywamy proste, które leżą na jednej płaszczyźnie i nie mają punktów wspólnych albo proste, które się pokrywają. ● Proste pokrywające się to proste, które mają wszystkie punkty wspólne. |
|
| Proste skośne | |
|
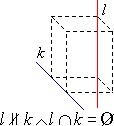
● Proste l i k w przestrzeni nazywamy skośnymi, jeżeli nie leżą na jednej płaszczyźnie - nie mają punktów wspólnych i nie są równoległe. ● Proste leżące na jednej płaszczyźnie mogą być równoległe lub przecinające się. ● Proste w przestrzeni mogą być równoległe, przecinające się lub skośne. |
|
| Kierunek prostych | |
|
● Zbiór wszystkich prostych równoległych do prostej l nazywamy kierunkiem prostej l i oznaczamy ( l ). |
|
| Pęk prostych | |
|
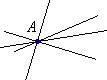
● Pękiem prostych o wierzchołku A nazywamy zbiór wszystkich prostych przechodzących przez punkt A i oznaczamy ( A ). |
|