| Własności funkcji trygonometrycznych w trójkącie prostokątnym | |||
|
|
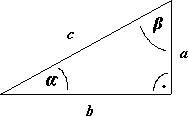
α , β - kąty ostre w trójkącie prostokątnym, c - przeciwprostokątna, a - przyprostokątna - bok trójkąta przeciwległy kątowi α (przyprostokątna przyległa do kąta β ) b - przyprostokątna - bok trójkąta przeciwległy kątowi β (przyprostokątna przyległa do kąta α ) |
||
|
● Sinusem kąta ostrego α w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przeciwległej temu kątowi do długości przeciwprostokątnej. |
|
||
|
● Cosinusem kąta ostrego α w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przyległej do tego kąta do długości przeciwprostokątnej. |
|
||
|
● Tangensem kąta ostrego α w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przeciwległej temu kątowi do długości drugiej przyprostokątnej. |
|
||
|
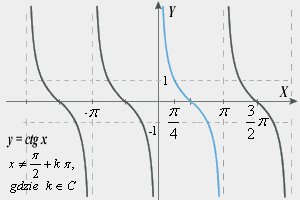
● Cotangensem kąta ostrego α w trójkącie prostokątnym nazywamy stosunek długości przyprostokątnej przyległej do tego kąta do długości drugiej przyprostokątnej. |
|
||
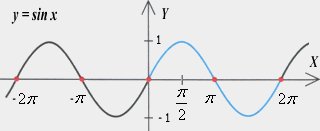
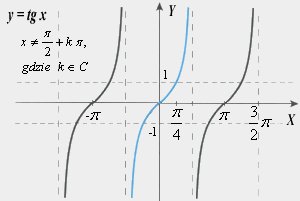
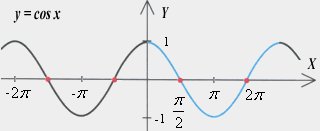
Wartości sinusów i cosinusów oraz tangensów i cotangensów
| Wpisz wielkość kąta dla szukanej wartości funkcji trygonometrycznej | |||
|
Uwaga! Wartość kąta podaj w zakresie od [-] 360 do 360º w stopniach w systemie dziesiętnym lub w stopniach i minutach w formacie "stopnie : minuty" |
|||
| Tabela wartości funkcji trygonometrycznych | |||
| Wartość sinusa | Wartość cosinusa | Wartość tangensa | Wartość cotangensa |
| sin( α ) = ? | cos( α ) = ? | tg( α ) = ? | ctg( α ) = ? |
| 0 | ||||||||||||||
| 0o | 15o | 22,5o | 30o | 45o | 60o | 90o | 120o | 135o | 150o | 180o | 225o | 270o | 360o | |
| sin α | 0 |
|
|
|
|
1 | 0 |
- |
- 1 | 0 | ||||
| cos α | 1 | 0 |
- |
- |
- |
- 1 |
- |
0 | 1 | |||||
| tg α | 0 | 1 | nie istn. |
- |
- 1 |
- |
0 | 1 | nie istn. |
0 | ||||
| ctg α | nie istn. |
1 | 0 |
- |
- 1 |
- |
nie istn. |
1 | 0 | nie istn. |
| 0 |
( 0; |
|
( |
|
( |
|
( |
|
|
| 0o | I ćw. | 90o | II ćw. | 180o | III ćw. | 270o | IV ćw. | 360o | |
| sinα | 0 |
|
1 |
|
0 |
|
- 1 |
|
0 |
| cosα | 1 |
|
0 |
|
- 1 |
|
0 |
|
1 |
| tgα | 0 |
|
nie |
|
0 |
|
nie |
|
0 |
| ctgα |
nie |
|
0 |
|
nie |
|
0 |
|
nie |
| I ćwiartka | II ćwiartka | III ćwiartka | IV ćwiartka |
wierszyk ułatwiający zapamiętanie: W pierwszej ćwiartce wszystkie są dodatnie |
|
| sinα | + | + | – | – | |
| cosα | + | – | – | + | |
| tgα | + | – | + | – | |
| ctgα | + | – | + | – |