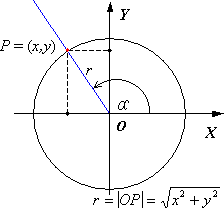| I ćwiartka | II ćwiartka | III ćwiartka | IV ćwiartka | |||||
| gdy φ = |
|
|
|
|
|
|
|
|
|
90o–α |
90o+α |
180o–α |
180o+α |
270o–α |
270o+α |
360o–α |
||
| sin φ = | cosα | cosα | sinα | - sinα | - cosα | - cosα | - sinα | |
| cos φ = | sinα | - sinα | - cosα | - cosα | - sinα | sinα | cosα | |
| tg φ = | ctgα | - ctgα | - tgα | tgα | ctgα | - ctgα | - tgα | |
| ctg φ = | tgα | - tgα | - ctgα | ctgα | tgα | - tgα | - ctgα | |
| Funkcje trygonometryczne kąta dowolnego | ||||
|
|
α - miara kąta skierowanego |OP| - promień wodzący punktu P gdzie P = ( x, y ) P - jest dowolnym punktem leżącym na końcowym ramieniu kąta skierowanego α |
|||
|
|
|
x ≠ 0 |
y ≠ 0 |
|
| Funkcje trygonometryczne tego samego kąta | |
|
sin2α + cos2α = 1 |
ctgα = |
|
tgα = |
tgα · ctgα = 1 , gdy sinα ≠ 0 i cosα ≠ 0 |
| Funkcje trygonometryczne podwojonego kąta | |
|
sin2α = 2sinα · cosα |
tg2α = |
|
cos2α = cos2α - sin2α = 1 - 2sin2α = 2cos2α - 1 |
ctg2α = |
| Funkcje trygonometryczne potrojonego kąta | |
|
sin3α = sinα ( 3cos2α - sin2α ) = sinα ( 3 - 4sin2α ) |
tg3α = |
|
cos3α = cosα ( cos2α - 3sin2α ) = cosα ( 4cos2α -3) |
ctg3α = |
| Funkcje trygonometryczne połowy kąta | |
|
znak "+" lub "-" zależy od tego, do której ćwiartki należy końcowe ramię kąta |
|
|
|
|
| Funkcje trygonometryczne sumy i różnicy kątów | |
|
sin( α + β ) = sinα · cosβ + cosα · sinβ |
tg( α + β ) = |
|
cos( α + β ) = cosα · cosβ - sinα · sinβ |
ctg( α + β ) = |
|
sin( α - β ) = sinα · cosβ - cosα · sinβ |
tg( α - β ) = |
|
cos( α - β ) = cosα · cosβ + sinα · sinβ |
ctg( α - β ) = |
| Suma i różnica funkcji trygonometrycznych | |
|
sinα + sinβ = 2sin |
tgα + tgβ = |
|
cosα + cosβ = 2cos |
ctgα + ctgβ = |
|
sinα - sinβ = 2sin |
tgα - tgβ = |
|
cosα - cosβ = -2sin |
ctgα - ctgβ = |
| Parzystość i nieparzystość funkcji trygonometrycznych | |
| sin ( – α ) = – sin α | tg ( – α ) = – tg α |
| cos ( – α ) = cos α | ctg ( – α ) = – ctg α |