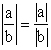|
●
● |x| ≥ 0 |
|
● Jeśli a > 0 to | x | ≤ a ⇔ –a ≤ x ≤ a |
|
● Jeśli a ≥ 0 to | x | ≥ a ⇔ ( x ≥ a lub x ≤ –a ) |
|
● |a + b| ≤ | a | + | b | ● |a – b| ≤ | a | + | b | ● |a · b| = | a | · | b | |
|
● |
|
● | |a| – |b| | ≤ | a + b | oraz | |a| – |b| | ≤ | a – b | |
|
● Jeden procent (1%) pewnej liczby a (lub innej wielkości), to setna część tej liczby (wielkości), co oznaczamy: 1% a |
|
|
1% a jest równe |
p% a jest równe |
|
Jeżeli liczba b stanowi p% liczby a to : |
|
|
|
|
|
a : b = c : d
wyrazy skrajne |
● Równość dwóch stosunków (ułamków) nazywamy proporcją. a : b = c : d lub |
|
● W proporcji iloczyn wyrazów skrajnych jest równy iloczynowi wyrazów środkowych, ● Jeżeli a : b = c : d to: dla: b ≠ 0 , d ≠ 0 , a ≠ ±b i c ≠ ±d . |
|
Dana liczba naturalna jest podzielna przez: |
|
| 2 |
gdy jej ostatnią cyfrą jest 0, 2, 4, 6 lub 8 |
| 3 |
gdy suma jej cyfr dzieli się przez 3 |
| 4 |
gdy liczba wyrażona dwiema ostatnimi jej cyframi, dzieli się przez 4 |
| 5 |
gdy jej ostatnią cyfrą jest 0 lub 5 |
| 6 |
gdy dzieli się przez 2 i przez 3 |
| 7 |
gdy różnica między liczbą wyrażoną kolejnymi trzema ostatnimi cyframi danej liczby a liczbą wyrażoną pozostałymi cyframi tej liczby (lub odwrotnie) dzieli się przez 7 |
| 8 |
gdy liczba wyrażona trzema ostatnimi jej cyframi dzieli się przez 8 |
| 9 |
gdy suma jej cyfr dzieli się przez 9 |
| 10 |
gdy ostatnią jej cyfrą jest 0 |
| 11 |
gdy różnica sumy jej cyfr stojących na miejscach parzystych i sumy cyfr stojących na miejscach nieparzystych dzieli się przez 11 |
|
Dodawanie: |
a + 0 = a 0 - element neutralny dodawania ● przemienność dodawania: a + b = b + a ● łączność dodawania: (a + b) + c = (a + ( b + c ) |
|
a + b = c składniki suma |
|
|
Odejmowanie: |
a – b = a + ( – b ) a – b = c ⇔ a = b + c ● odejmowanie jest działaniem odwrotnym do dodawania |
|
a – b = c odjemna różnica |
|
|
Mnożenie: |
a · 1 = a 1 - element neutralny mnożenia ● przemienność mnożenie: a · b = b · a ● łączność mnożenia: (a · b) · c = a · (b · c) ● rozdzielność mnożenia względem dodawania: a · ( b + c ) = a · b + a · c |
|
a · b = c czynniki iloczyn |
|
|
Dzielenie: |
a : b = c ⇔ a = b · c ● dzielenie jest działaniem odwrotnym do mnożenia |
|
a : b = c dzielnailoraz dzielnik |