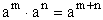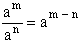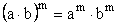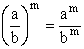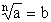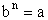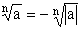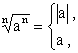|
Potęgowanie |
|
|
|
an- n-ta potęga liczby a n - wykładnik potęgi b - wynik potęgowania |
|
Potęga o wykładniku naturalnym |
|
|
● ● ● Jeżeli a ∈ R ∧ n ∈ N \ { 0 } to: |
|
|
Potęga o wykładniku całkowitym ujemnym |
|
|
● ● |
|
|
Potęga o wykładniku wymiernym dodatnim |
|
|
● |
gdzie a ∈ R+∪ { 0 } m ∈ N+ i n ∈ N+ \ { 1 } |
|
Potęga o wykładniku wymiernym ujemnym |
|
|
● |
gdzie a ∈ R+ m ∈ N+ i n ∈ N+ \ { 1 } |
|
Jeżeli m, n ∈ R i a, b ∈ R+ albo m, n ∈ C i a, b ∈ R i a ≠ 0 i b ≠ 0 to: |
|
|
● |
iloczyn potęg o tych samych podstawach |
|
● |
iloraz potęg o tych samych podstawach |
|
● |
potęga iloczynu |
|
● |
potęga ilorazu |
|
● |
potęga potęgi |
|
Pierwiastkowanie |
|
|
|
a - liczba podpierwiastkowa b - pierwiastek n-tego stopnia z a n - stopień pierwiastka |
|
● Jeżeli a ≥ 0 , b ≥ 0 i n ∈ N \ { 0, 1 }, to:
● Jeżeli a < 0 i n = 2k + 1 gdzie k ∈ N + to:
|
|
|
Prawa działań na pierwiastkach |
||
|
● Jeżeli a ≥ 0 , b ≥ 0 i n ∈ N \ { 0,1 } i m ∈ N \ { 0,1 } , to: |
||
|
● |
● |
|
|
● |
● |
|
|
● |
● |
|
|
● |
||
|
● ● |
||
|
Wyrażenie algebraiczne |
|
● Liczbę, literę lub liczby, litery lub liczby i litery połączone znakami działań, nawiasami, nazywamy wyrażeniami algebraicznymi. |
|
Kolejność wykonywania działań |
|
● Litery występujące w wyrażeniu algebraicznym nazywamy zmiennymi. Jeżeli w wyrażeniu algebraicznym nie ma nawiasów, to kolejność wykonywania działań jest następująca: potęgowanie i pierwiastkowanie potem mnożenie i dzielenie (w kolejności występowania) a następnie dodawanie i odejmowanie. |
|
● Przy obliczaniu wartości wyrażeń zawierających nawiasy -najpierw wykonujemy działania w tych nawiasach, wewnątrz których nie ma innych nawiasów. |