| Stosowane oznaczenia | ||
|
X = Df - dziedzina funkcji f, Y - przeciwdziedzina funkcji, f : X → Y
|
x - argument funkcji f, zmienna niezależna y, f ( x ) - wartość funkcji f, zmienna zależna f, g, h ... - symbole funkcji |
|
| Pojęcie funkcji | ||
| f : X → Y
odwzorowanie zbioru X |
● Funkcją f odwzorowującą zbiór X w zbiór Y nazywamy takie przyporządkowanie, które każdemu elementowi x ze zbioru X przyporządkowuje dokładnie jeden element y ze zbioru Y . |
|
|
● Odwzorowując w sposób opisany zbiór X w zbiór Y tworzymy zbiór uporządkowanych par ( x, y ), czyli par ( x, f ( x )), Zbiór tych par jest podzbiorem iloczynu kartezjańskiego X × Y |
||
|
f : X → Y odwzorowanie zbioru X |
● Jeżeli f : X → Y i |
|
| Zbiór wartości funkcji | ||
|
● Jeżeli f : X → Y to zbiór |
||
|
|
||
| Miejsca zerowe funkcji | |
|
● Miejscem zerowym funkcji y = f ( x ) nazywamy każdą wartość argumentu x, dla której wartość funkcji y równa jest zero. |
|
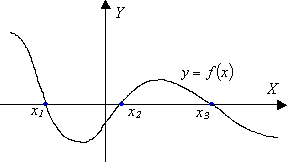 |
Miejsce zerowe funkcji y = f ( x ) wyznaczamy rozwiązując równanie f ( x ) = 0 , ● Każde rozwiązanie równania f ( x ) = 0 należące do Df jest miejscem zerowym funkcji f . Miejsce zerowe funkcji f jest równe odciętej punktu wykresu funkcji leżącego na osi X . |
| Równość funkcji |
|
● Dwie funkcje f i g są równe wtedy i tylko wtedy, gdy: Df = Dg = D i f ( x ) = g ( x ) dla każdego x ∈ D |
| Funkcja różnowartościowa |
|
● Funkcję f : X → Y, która każdej parze różnych argumentów przyporządkowuje różne wartości, to znaczy taką, że |
|
● Określając różnowartościowość funkcji f sprawdzamy, czy spełniony jest warunek f ( x1 ) − f ( x2 ) ≠ 0 |
|
● Jeżeli funkcja f jest różnowartościowa, to każda prosta y = m ( gdzie m ∈ R ) ma co najwyżej jeden punkt wspólny z wykresem funkcji f . |
|
● Każda funkcja ściśle monotoniczna jest różnowartościowa. |
| Funkcja odwrotna |
|
● Jeśli funkcja f : X → Y, jest różnowartościowa to funkcję f −1 : Y → X określoną następująco: dla dowolnego y ∈ Y wartością f −1 ( y ) jest jedyny element x ∈ X taki, że f ( x ) = y , nazywamy odwrotną do funkcji f. f −1 ( y ) = x ⇔ f ( x ) = y |
|
● Funkcją odwrotną do f −1 jest funkcja f . |
|
● Jeżeli funkcja f ma funkcję odwrotną f −1 , to funkcję f nazywamy funkcją odwracalną. |

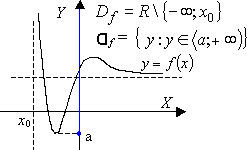 Jeżeli
Jeżeli