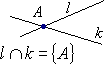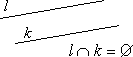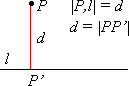| Równanie ogólne prostej | |
|
postać równania l : Ax + By + C = 0 A , B , C - współczynniki liczbowe równania prostej Jeżeli B ≠ 0 , to l : Jeżeli B = 0 to l : Jeżeli B ≠ 0 i A = 0 to l : |
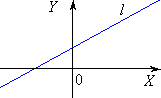 l : Ax + By + C = 0 |
| Równanie kierunkowe prostej | |
|
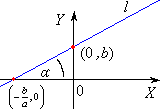
postać równania l : y = ax + b
gdzie: A, B, C - współczynniki liczbowe równania prostej a = tg α - współczynnik kierunkowy |
 |
| ● Równania prostej prostopadłej do osi OX nie można przedstawić w postaci kierunkowej. | |
| Równanie prostej przechodzącej przez punkt A płaszczyzny | |
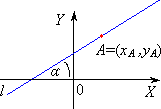
| postać równania l : y - yA = a ( x - xA ) a - współczynnik kierunkowy prostej l a = tg α |
 |
| Równanie prostej przechodzącej przez dwa różne punkty A i B płaszczyzny | |
|
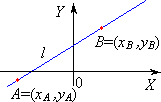
postać równania prostej l : gdy: |
 |
| postać równania prostej k : x = a , gdy: xA = xB = a | 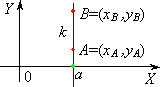 |
| Półproste | |
|
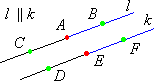
● Półprostą o początku A nazywamy każdą z dwóch części prostej, na które punkt A dzieli tę prostą, wraz z tym punktem. Takie dwie półproste nazywamy półprostymi dopełniającymi się. ● Jeżeli punkt A leży między punktami B i C, to: AB → ∩ AC → = { A } AB → ∪ AC → = l Półproste dopełniające się - półproste AB → i AC → Dwie półproste zgodnie zorientowane - o zgodnym zwrocie - Dwie półproste przeciwnie zorientowane, |
|
| Proste przecinające się | |
|
● Prostymi przecinającymi się nazywamy proste, które mają dokładnie jeden punkt wspólny. |
|
| Proste równoległe | |
|
● Prostymi równoległymi nazywamy proste, które leżą na jednej płaszczyźnie i nie mają punktów wspólnych albo proste, które się pokrywają. ● Proste pokrywające się to proste, które mają wszystkie punkty wspólne. |
|
| Proste skośne | |
|
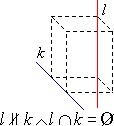
● Proste l i k w przestrzeni nazywamy skośnymi, jeżeli nie leżą na jednej płaszczyźnie - nie mają punktów wspólnych i nie są równoległe. ● Proste leżące na jednej płaszczyźnie mogą być równoległe lub przecinające się. ● Proste w przestrzeni mogą być równoległe, przecinające się lub skośne. |
|
| Kierunek prostych | |
|
● Zbiór wszystkich prostych równoległych do prostej l nazywamy kierunkiem prostej l i oznaczamy ( l ). |
|
| Pęk prostych | |
|
● Pękiem prostych o wierzchołku A nazywamy zbiór wszystkich prostych przechodzących przez punkt A i oznaczamy ( A ). |
|
|
● Pojęcie, które przyjmuje się bez definicji nazywamy pojęciem pierwotnym. |
|
|
● Pojęcie pierwotne w geometrii, to punkt, prosta, płaszczyzna, przestrzeń. |
|
|
● Aksjomat to zdanie, którego prawdziwość przyjmuje się bez dowodu. |
|
|
Przykłady aksjomatów w geometrii płaszczyzny: - Przez każdy punkt płaszczyzny przechodzi nieskończenie wiele prostych. - Przez każde dwa różne punkty przechodzi dokładnie jedna prosta. - Przez punkt nie leżący na prostej l przechodzi dokładnie jedna prosta k równoległa do prostej l , to tzw. aksjomat Euklidesa. |
|
|
Przykłady aksjomatów w geometrii przestrzeni: - Przez każde dwa punkty przestrzeni przechodzi nieskończenie wiele płaszczyzn. - Przez każde trzy punkty, nie należące do jednej prostej, przechodzi dokładnie jedna płaszczyzna. - Przez punkt nie leżący na płaszczyźnie α przechodzi dokładnie jedna płaszczyzna β równoległa do płaszczyzny α . |
|
| Odległość punktu od prostej | |
|
● Odległość d punktu P od prostej l jest równa odległości tego punktu od jego rzutu prostokątnego P' na prostą l. |
|
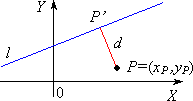
| Odległość punktu od prostej w układzie współrzędnych na płaszczyźnie | |
|
równanie prostej l : Ax + By + C = 0 gdzie A 2 + B 2 > 0 Jeżeli | P,l | = | PP' | = d , to
|
|